Decision Making for a Single Sample

Yi-Ju Tseng

Import Packages and Data

Packages installation

In CMD (Windows) or terminal (Mac or Linux), type

pip3 install statsmodels random

to install packages

Of course you can use conda or other method to install packages

Import packages

We will use the following packages in python.

  • statistics, pandas, seaborn, numpy, random, math, statsmodels, scipy
import statistics as st
import pandas as pd
import seaborn as sns
import random
from scipy import stats
import numpy as np
import math
import statsmodels.stats.power as power
from statsmodels.stats.weightstats import ztest as ztest
from statsmodels.stats.proportion import proportions_ztest as proportions_ztest
from statsmodels.stats.proportion import proportion_confint as proportion_confint

Import data

Import data and analyze with python using pandas. pd.read_csv("file path + name")

data = pd.read_csv("baseball_data.csv")
data
name handedness height weight bavg HR
0 Jose Cardenal Right 70 150 0.275 138
1 Darrell Evans Left 74 200 0.248 414
2 Buck Martinez Right 70 190 0.225 58
3 John Wockenfuss Right 72 190 0.262 86
4 Tommy McCraw Left 72 183 0.246 75
... ... ... ... ... ... ...
300 Bob Watson Right 72 201 0.295 184
301 Ken Harrelson Right 74 190 0.239 131
302 Ed Charles Right 70 170 0.263 86
303 Tony Conigliaro Right 75 185 0.264 166
304 Phil Garner Right 70 175 0.260 109

305 rows × 6 columns

Describe the data

data.describe()
height weight bavg HR
count 305.000000 305.000000 305.00000 305.000000
mean 72.806557 187.449180 0.26142 139.426230
std 1.795084 15.439766 0.01889 91.206363
min 67.000000 150.000000 0.21200 50.000000
25% 72.000000 175.000000 0.24800 76.000000
50% 73.000000 190.000000 0.26000 109.000000
75% 74.000000 195.000000 0.27400 173.000000
max 78.000000 230.000000 0.32800 563.000000

Sampling Distribution

Central Limit Theorem - population distribution

sns.histplot(data=data, x="HR", binwidth=5)
<Axes: xlabel='HR', ylabel='Count'>

Central Limit Theorem - population distribution

With scipy package’s stats:

  • Shapiro-Wilk Test shapiro(data)

    • May not be accurate for N > 5000
    • If the p-value > .05, then the data is assumed to be normally distributed.
    stats.shapiro(data["HR"])
    ShapiroResult(statistic=0.8178355097770691, pvalue=3.0833140789301856e-18)

  • p-value < 0.05, HR is not normally distributed.

Sampling, n=3, one time

With random’s random.sample(data,n) function, we can randomly select n samples from the population

samp=random.sample(list(data["HR"]), 3)
samp
[218, 82, 253]

Then we can get the mean of the samples

st.mean(samp)
184.33333333333334

Sampling, n=3, many times

Perform sampling 1000 times

samp1000=[random.sample(list(data["HR"]), 3) for i in range(1000)]
samp1000=np.array(samp1000)
samp1000
array([[122, 121, 159],
       [ 78,  80, 306],
       [130, 184, 118],
       ...,
       [ 65, 189,  65],
       [121, 255, 102],
       [ 63,  91, 241]])

Sampling, n=3, many times

  1. calculate the sample mean for the 1000 times of sampling (get 1000 sample means)
  2. plot the Sampling distribution of the sample mean
nsamp1000mean=np.mean(samp1000,axis=1)
sns.histplot(data=nsamp1000mean, binwidth=5)
<Axes: ylabel='Count'>

Sampling, n=3, many times

Sampling distribution of the sample mean - mean

The mean of sample mean vs. the population mean

np.mean(nsamp1000mean)
138.575
data["HR"].mean()
139.4262295081967

Sampling, n=3, many times

Sampling distribution of the sample mean - sd (standard error)

The sd of sample mean vs. the estimated standard error

np.std(nsamp1000mean)
51.14300144909587
data["HR"].std()/(math.sqrt(3))
52.658018147094694

Sampling, n=30, many times

Sampling with n=30, 1000 times

samp1000=[random.sample(list(data["HR"]), 30) for i in range(1000)]
samp1000=np.array(samp1000)
samp1000
array([[ 61,  56, 390, ...,  61, 242,  95],
       [ 61,  91, 234, ..., 442, 101,  81],
       [191, 110, 203, ...,  81,  82, 160],
       ...,
       [121,  83,  76, ..., 112,  61,  63],
       [389,  86,  65, ...,  87,  85,  52],
       [271, 134,  66, ..., 195,  50,  96]])

Sampling, n=30, many times

  1. get 1000 sample mean for the 1000 times of sampling
  2. plot the Sampling distribution of the sample mean
nsamp1000mean=np.mean(samp1000,axis=1)
sns.histplot(data=nsamp1000mean, binwidth=5)
<Axes: ylabel='Count'>

Sampling, n=30, many times

Sampling distribution of the sample mean - mean

The mean of sample mean vs. the population mean

np.mean(nsamp1000mean)
138.61176666666668
data["HR"].mean()
139.4262295081967

Sampling, n=30, many times

Sampling distribution of the sample mean - sd (standard error)

The sd of sample mean vs. the estimated standard error

np.std(nsamp1000mean)
15.986923141916819
data["HR"].std()/(math.sqrt(30))
16.651927441529864

Central Limit Theorem - population distribution

sns.histplot(data=data, x="HR", binwidth=5)
<Axes: xlabel='HR', ylabel='Count'>

Sampling, n=30, many times

nsamp1000mean=np.mean(samp1000,axis=1)
sns.histplot(data=nsamp1000mean, binwidth=5)
<Axes: ylabel='Count'>

Confidence Interval

95% of Confidence Interval

The idea of confidence interval (CI)…

  • CI is a range of estimates for an unknown parameter
  • 95% CI = out of all intervals computed at the 95% level, 95% of them should contain the parameter’s true value

True value of the mean of #HR

data["HR"].mean()
139.4262295081967

Simulation (95% CI)

Sampling 1000 times (with n=30)

samp1000=[random.sample(list(data["HR"]), 30) for i in range(1000)]
samp1000=np.array(samp1000)
samp1000
array([[100, 200, 160, ..., 235,  66,  65],
       [292, 113,  50, ..., 414, 251, 121],
       [147,  81,  52, ..., 563, 207,  95],
       ...,
       [153, 134,  71, ..., 166, 155,  63],
       [196,  85, 116, ..., 122, 113,  87],
       [189, 121, 160, ...,  52,  72, 102]])

Simulation (95% CI)

stats.norm.interval(confidence,loc=point estimation, scale=standard error)

stats.norm.interval(confidence=0.95,\
loc=np.mean(samp1000[1]), scale=data["HR"].std()/math.sqrt(30))
(109.06282194142725, 174.33717805857273)
stats.norm.interval(confidence=0.95, \
loc=np.mean(samp1000[2]), scale=data["HR"].std()/math.sqrt(30))
(119.99615527476058, 185.27051139190607)
stats.norm.interval(confidence=0.95, \
loc=np.mean(samp1000[3]), scale=data["HR"].std()/math.sqrt(30))
(94.62948860809394, 159.9038447252394)

…

95% of them should contain the parameter’s true value (=139)

Simulation (95% CI)

ci1000=[stats.norm.interval(confidence=0.95,\
loc=np.mean(samp1000[i]), \
scale=data["HR"].std()/math.sqrt(30)) for i in range(1000)]

n=0
for i in range(1000):
    if data["HR"].mean()<ci1000[i][0] or \
    data["HR"].mean()>ci1000[i][1]:
      print(ci1000[i])
      n+=1

print(n)
print((1000-n)/1000)
(70.16282194142727, 135.43717805857273)
(149.1961552747606, 214.4705113919061)
(144.06282194142725, 209.33717805857273)
(179.3961552747606, 244.67051139190608)
(144.42948860809392, 209.7038447252394)
(140.7961552747606, 206.07051139190608)
(140.8961552747606, 206.17051139190608)
(146.26282194142726, 211.53717805857275)
(68.16282194142727, 133.43717805857273)
(157.09615527476058, 222.37051139190606)
(70.99615527476061, 136.27051139190607)
(144.26282194142726, 209.53717805857275)
(143.42948860809392, 208.7038447252394)
(146.0294886080939, 211.3038447252394)
(70.92948860809392, 136.2038447252394)
(139.92948860809392, 205.2038447252394)
(66.7961552747606, 132.07051139190608)
(141.56282194142725, 206.83717805857273)
(141.96282194142725, 207.23717805857274)
(65.26282194142726, 130.53717805857275)
(69.49615527476061, 134.77051139190607)
(73.92948860809392, 139.2038447252394)
(146.42948860809392, 211.7038447252394)
(142.82948860809392, 208.1038447252394)
(144.16282194142727, 209.43717805857275)
(139.42948860809392, 204.7038447252394)
(143.16282194142727, 208.43717805857275)
(74.02948860809394, 139.3038447252394)
(73.5961552747606, 138.87051139190606)
(144.32948860809392, 209.6038447252394)
(145.32948860809392, 210.6038447252394)
(74.06282194142727, 139.33717805857273)
(144.0294886080939, 209.3038447252394)
(150.7961552747606, 216.07051139190608)
(70.22948860809393, 135.5038447252394)
(140.2961552747606, 205.57051139190608)
(73.26282194142726, 138.53717805857275)
(70.5961552747606, 135.87051139190606)
(142.3961552747606, 207.67051139190608)
(150.82948860809392, 216.1038447252394)
(70.66282194142727, 135.93717805857273)
(67.52948860809394, 132.8038447252394)
(144.99615527476058, 210.27051139190607)
(68.62948860809394, 133.9038447252394)
(69.46282194142725, 134.73717805857274)
(140.86282194142726, 206.13717805857274)
(72.89615527476059, 138.17051139190608)
(140.0294886080939, 205.3038447252394)
(141.26282194142726, 206.53717805857275)
(139.42948860809392, 204.7038447252394)
50
0.95

Simulation (95% CI)

print(n)
print((1000-n)/1000)
50
0.95

z-test

Check the data

sns.histplot(data=data, x="bavg", binwidth=0.01)
<Axes: xlabel='bavg', ylabel='Count'>

Normally distributed?

Shapiro-Wilk Test

With scipy package’s stats, the following functions can be used:

  • Shapiro-Wilk Test shapiro(data)
    • May not be accurate for N > 5000
    • If the p-value > .05, then the data is assumed to be normally distributed.
stats.shapiro(data["bavg"])
ShapiroResult(statistic=0.994293212890625, pvalue=0.3108234703540802)
  • p-value > .05, average batting rate is normally distributed.

Two-sided z-test, small sample

  • H0: The average batting rate = 0.25
  • H1: The average batting rate != 0.25
data["bavg"].std() # population sd
0.018889766963749978
samp9=random.sample(list(data["bavg"]), 9) # sampling 
st.stdev(samp9) # sample sd
0.014584047601555761

Two-sided z-test, small sample

  • Use the formula directly
(st.mean(samp9)-0.25)/(data["bavg"].std()/math.sqrt(9)) # z value
2.823398162385041

Two-sided z-test, small sample

  • ztest(data=your data,value=the value you want to compare with) from statsmodels.stats.weightstats, but this function use sd from samples, not population
  • return (test statistic, p-value)
ztest(samp9, value=0.25) #z value with sample sd
(3.656963744937584, 0.00025522046217604463)
(st.mean(samp9)-0.25)/(st.stdev(samp9)/math.sqrt(9)) # z value
3.656963744937584
  • P>0.05, fail to reject H0, there is no evidence that average batting rate is not 0.25

Population sd vs. sample sd, large n

n=30

data["bavg"].std() # population sd
0.018889766963749978
samp1000=[random.sample(list(data["bavg"]), 30) for i in range(1000)]
samp1000=np.array(samp1000)
samp1000sd=np.std(samp1000,axis=1)
np.mean(samp1000sd) # sample sd, average
0.01842008267792998

Population sd vs. sample sd, large n

n=30

sns.histplot(samp1000sd, binwidth=0.001)
<Axes: ylabel='Count'>

Population sd vs. sample sd, small n

n=9

data["bavg"].std() # population sd
0.018889766963749978
samp1000=[random.sample(list(data["bavg"]), 9) for i in range(1000)]
samp1000=np.array(samp1000)
samp1000sd=np.std(samp1000,axis=1)
np.mean(samp1000sd) # sample sd, average
0.017060516763831367

Population sd vs. sample sd, small n

n=9

sns.histplot(samp1000sd, binwidth=0.001)
<Axes: ylabel='Count'>

Two-sided z-test, large sample

population sd

data["bavg"].std() # population sd
0.018889766963749978

sample sd

samp30=random.sample(list(data["bavg"]), 30) # sampling 
st.stdev(samp30) # sample sd
0.018857877405208816

Two-sided z-test, large sample

  • Use the formula directly
(st.mean(samp30)-0.25)/(data["bavg"].std()/math.sqrt(30)) # z value
2.0200357639537305

Two-sided z-test, large sample

  • ztest(data=your data,value=the value you want to compare with) from statsmodels.stats.weightstats, but this function use sd from samples, not population
  • return (test statistic, p-value)
ztest(samp30, value=0.25) #z value with sample sd
(2.0234517395360117, 0.04302659444666302)
  • P<0.05, reject H0, there is evidence that average batting rate is not 0.25

One-sided

  • ztest(data=your data,value=the value you want to compare with,alternative=side) from statsmodels.stats.weightstats
  • alternative="smaller" or alternative="larger"
  • assume that data['bavg'] are the samples you want to test
ztest(data['bavg'], value=0.25)
(10.557885664986959, 4.670634306392867e-26)
ztest(data['bavg'], value=0.25, alternative="larger")
(10.557885664986959, 2.3353171531964336e-26)
ztest(data['bavg'], value=0.25, alternative="smaller")
(10.557885664986959, 1.0)

t-test

When to use z-test vs. t-test?

  • Target parameter: mean

t-test:

  • Sample size <30
  • Population fit normal distribution
  • Population sd unknown

z-test:

  • Sample size >=30 and Population can be any distribution
  • Sample size <30 and Population fit normal distribution and Population sd known

When to use z-test vs. t-test?

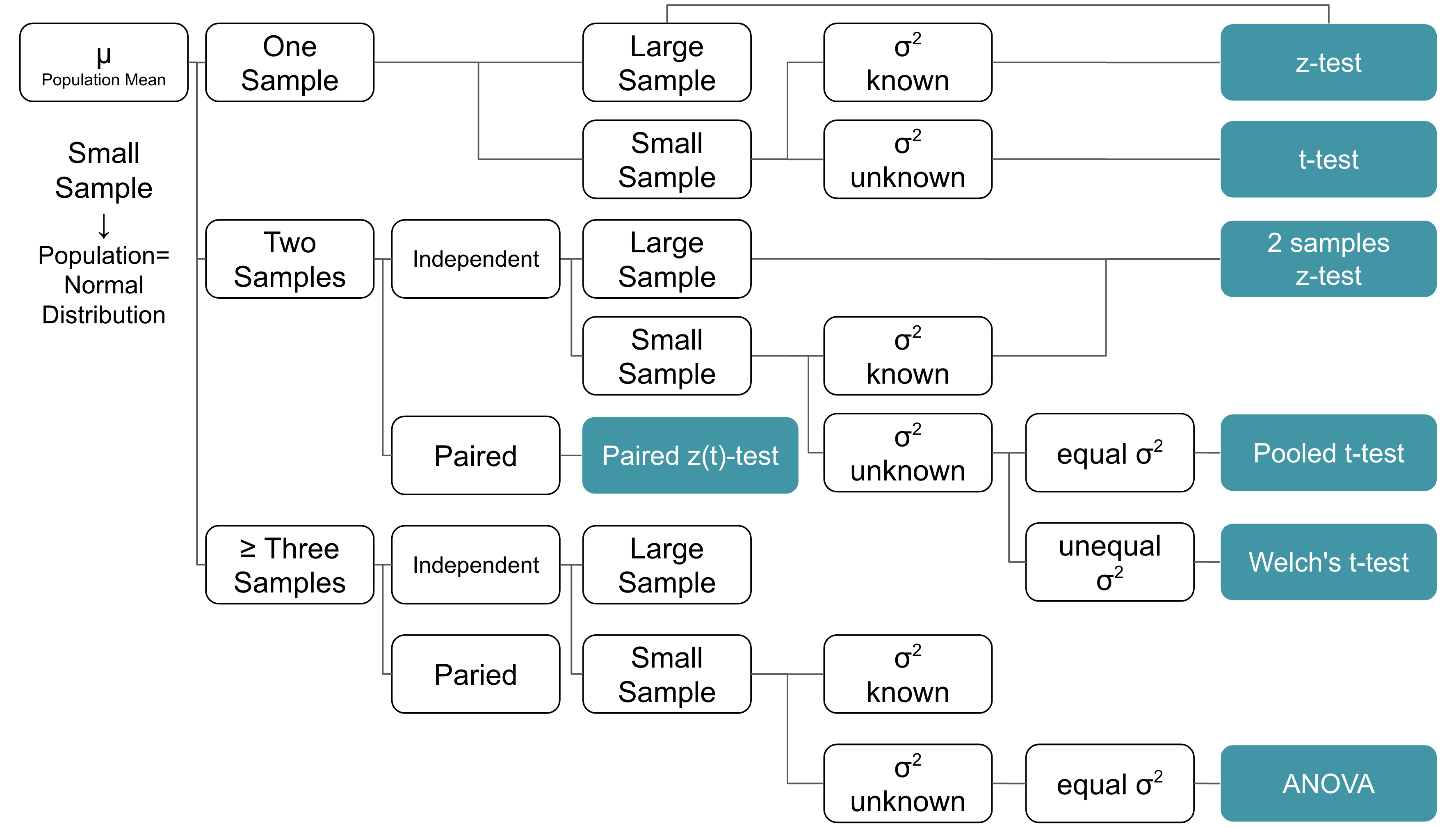
Check the data

sns.histplot(data=data, x="bavg", binwidth=0.01)
<Axes: xlabel='bavg', ylabel='Count'>

Normally distributed?

Shapiro-Wilk Test

With scipy package’s stats, the following functions can be used:

  • Shapiro-Wilk Test shapiro(data)
    • May not be accurate for N > 5000
    • If the p-value > .05, then the data is assumed to be normally distributed.
stats.shapiro(data["bavg"])
ShapiroResult(statistic=0.994293212890625, pvalue=0.3108234703540802)
  • p-value > .05, average batting rate is normally distributed.

Two-sided t-test, small sample

  • H0: The average batting rate = 0.25
  • H1: The average batting rate != 0.25
  • Sample size = 9 (small sample)
  • pretend that we don’t know population sd
data["bavg"].std() # population sd
0.018889766963749978
samp9=random.sample(list(data["bavg"]), 9) # sampling 
st.stdev(samp9) # sample sd
0.019104973174542794

Two-sided t-test, small sample

  • ttest_1samp(data=your data,popmean=the value you want to compare with) from scipy.stats
  • return (test statistic, p-value, degree of freedom)
stats.ttest_1samp(samp9, popmean=0.25) #t value with sample sd
TtestResult(statistic=4.0303642039446474, pvalue=0.0037861383037887638, df=8)
  • P>0.05, fail to reject H0, there is no evidence that average batting rate is not 0.25
  • P<0.05, reject H0, there is evidence that average batting rate is not 0.25

Two-sided t-test vs. z-test

ztest(samp9, value=0.25) #z value with sample sd
(4.0303642039446474, 5.569049551371776e-05)
stats.ttest_1samp(samp9, popmean=0.25) #t value with sample sd
TtestResult(statistic=4.0303642039446474, pvalue=0.0037861383037887638, df=8)

One-sided t-test

  • ttest_1samp(data=your data,popmean=the value you want to compare with,alternative="side") from scipy.stats
  • alternative="less" or alternative="greater"
st.mean(samp9)
0.27566666666666667
stats.ttest_1samp(samp9, popmean=0.25) 
TtestResult(statistic=4.0303642039446474, pvalue=0.0037861383037887638, df=8)
stats.ttest_1samp(samp9, popmean=0.25, alternative="greater") 
TtestResult(statistic=4.0303642039446474, pvalue=0.0018930691518943819, df=8)
stats.ttest_1samp(samp9, popmean=0.25, alternative="less")
TtestResult(statistic=4.0303642039446474, pvalue=0.9981069308481056, df=8)

Inference on the Variance - Chi-square distribution

Criteria for using chi-square distribution to infer variance

  • Target parameter: variance
  • Sample size large or small
  • Population is normal distribution

Chi-square distribution - probability

  • No single-step function
  • Calculate chi-square statistic first
  • Then use stats.chi2.ppf(alpha / 2, df) from scipy to get critical value
alpha=0.05
df=10
stats.chi2.ppf(alpha / 2, df)
3.2469727802368413
stats.chi2.ppf(1 - alpha / 2, df)
20.483177350807388

Hypothesis testing on variance

Example 4-6.3

Is the variation in boxes of cereal, measured by the variance, equal to 15 grams? A random sample of 25 boxes had a standard deviation of 17.7 grams. Test at the .05 level of significance.

  • H0: variance = 15
  • H1: variance != 15
chi=(25-1)*((17.7)**2)/(15**2)
chi
33.41759999999999

Hypothesis testing on variance

Example 4-6.3

stats.chi2.ppf(0.05/2, 25-1)
12.401150217444435
stats.chi2.ppf(1-0.05/2, 25-1)
39.36407702660391

chi=33.4 is within 12.4~39.4. Fail to reject H0. There is no evidence that variance is not 15

Confidence interval on variance inference

Example 4-6.2

n=10 # sample size
s2=16 # sample variance
alpha=0.05 
df=n-1
upper = (n - 1) * s2 / stats.chi2.ppf(alpha / 2, df)
lower = (n - 1) * s2 / stats.chi2.ppf(1 - alpha / 2, df)
(lower,upper)
(7.569876346295027, 53.32564061630642)

Inference on Popuation Proportion - z-test

Criteria for using z-test to popuation proportion

  • sample size n is large
  • np>=15 and nq>=15

Check the data

samp40=random.sample(list(data["handedness"]), 40) # sampling 
samp40
['Left',
 'Left',
 'Right',
 'Right',
 'Left',
 'Right',
 'Right',
 'Left',
 'Right',
 'Right',
 'Right',
 'Both',
 'Left',
 'Right',
 'Right',
 'Right',
 'Right',
 'Right',
 'Right',
 'Right',
 'Right',
 'Left',
 'Left',
 'Left',
 'Left',
 'Right',
 'Right',
 'Left',
 'Right',
 'Left',
 'Both',
 'Right',
 'Right',
 'Left',
 'Right',
 'Left',
 'Right',
 'Left',
 'Left',
 'Right']

Check the data

Left-hander

samp40.count('Left')
15

Proportion:

p=samp40.count('Left')/len(samp40)
p
0.375

Check np and nq

p*len(samp40)
15.0
(1-p)*len(samp40)
25.0

Confidence interval on popuation proportion

  • proportion_confint(count, n, alpha) function from statsmodels.stats.proportion
  • return (ci_low, ci_upp)
from statsmodels.stats.proportion import proportion_confint
proportion_confint(samp40.count('Left'),len(samp40), alpha=0.05)
(0.22497151011389654, 0.5250284898861035)

Confidence interval on popuation proportion

Example 4-14 (4-7.3)

  • 85 automobile
  • 10 have a surface finish rougher than allowed
proportion_confint(10,85, alpha=0.05)
(0.049153405048878565, 0.18614071259818027)

Hypothesis testing on popuation proportion

from statsmodels.stats.proportion import proportions_ztest

  • proportions_ztest(count, nobs, value=set proportion,prop_var=set proportion) from statsmodels.stats.proportion

  • return (test statistic, p value)

  • H0: % of left-hander = 0.3

  • H1: % of left-hander != 0.3

proportions_ztest(samp40.count('Left'),len(samp40),0.3,prop_var=0.3)
(1.0350983390135315, 0.3006229881969067)
  • P>0.05, fail to reject H0, there is no evidence that % of left-hander is not 0.3

Hypothesis testing on popuation proportion

  • proportions_ztest(count, nobs, value=set proportion,prop_var=set proportion) from statsmodels.stats.proportion

  • return (test statistic, p value)

  • H0: % of left-hander = 0.1

  • H1: % of left-hander != 0.1

proportions_ztest(samp40.count('Left'),len(samp40),0.1,prop_var=0.1)
(5.7975090436420285, 6.730715233582355e-09)
  • P<0.05, reject H0, there is evidence that % of left-hander is not 0.1

Hypothesis testing on popuation proportion

Example 4-12 (4-7.1) Random sample of 200, 4 of them are defective. Fraction defective not exceed 0.05.

  • H0: p>=0.05
  • H1: p<0.05
5/200 # proportion from sampling
0.025

One-sided test

proportions_ztest(4,200,0.05,alternative="smaller",prop_var=0.05)
(-1.9466570535691505, 0.0257879318104385)
  • P<0.05, reject H0, there is evidence that fraction defective not exceed 0.05

Goodness-of-fit test

Unknown distribution?

  • Compare data to a distribution family
  • Chi-square distribution

Goodness-of-fit test

Example 4-10

stats.chisquare(f_obs=observed, f_exp=expected, ddof=df) from scipy

observed=[32, 15, 13]
expected=[28.32, 21.24, 10.44]
stats.chisquare(f_obs=observed, f_exp=expected, ddof=1)
Power_divergenceResult(statistic=2.939151892980063, pvalue=0.08645611643144485)

Summary

Summary -1

Hypothesis test for single sample

  • z-test for population mean
    • ztest(data=your data,value=the value you want to compare with) from statsmodels.stats.weightstats
  • t-test for population mean
    • ttest_1samp(data=your data,popmean=the value you want to compare with) from scipy.stats

Summary -2

Hypothesis test for single sample

  • chi-square distribution for population variance
    • no easy to use function
    • stats.chi2.ppf(alpha / 2, df) from scipy
  • z-test for population proportion
    • proportions_ztest(count, nobs, value=set proportion,prop_var=set proportion) from statsmodels.stats.proportion