Random Variable and Distribution
Import Packages
Import packages/libraries
We will use the following packages in python.
statisticspandasscipyseabornnumpy
Normal Distribution - Continuous Random Variables
Probability (area under the pdf)

statistic (as st) package’s function:
NormalDist(mu=μ, sigma=σ).cdf(x)
Probability (area under the pdf)

Quiz 3-3
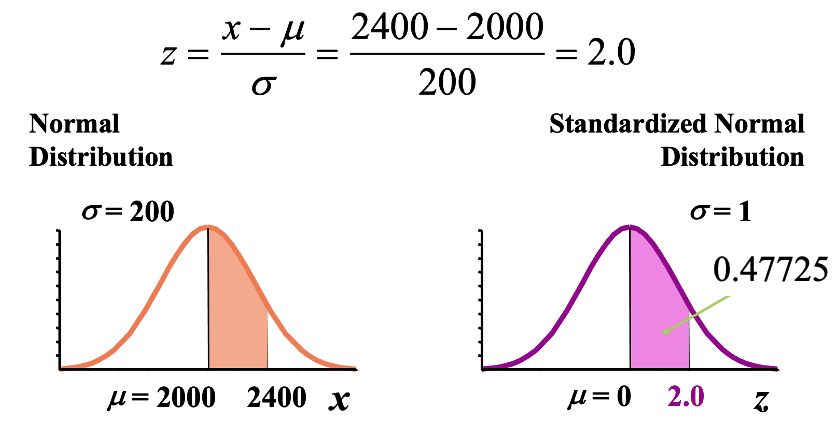
You work in Quality Control for GE.
Light bulb life has a normal distribution with μ = 2000 hours and σ = 200 hours.
What’s the probability that a bulb will last
A. between 2000 and 2400 hours?
Quiz 3-3
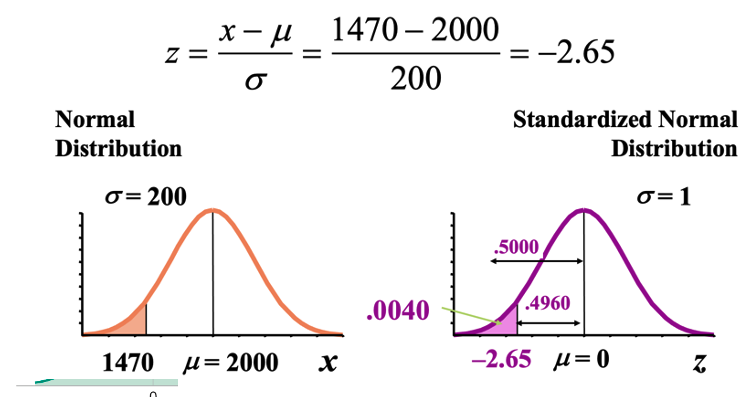
You work in Quality Control for GE.
Light bulb life has a normal distribution with μ = 2000 hours and σ = 200 hours.
What’s the probability that a bulb will last
B. less than 1470 hours?
Finding z-Values for Known Probabilities
statistic (as st) package’s function
NormalDist(mu=μ, sigma=σ).inv_cdf(p-value)
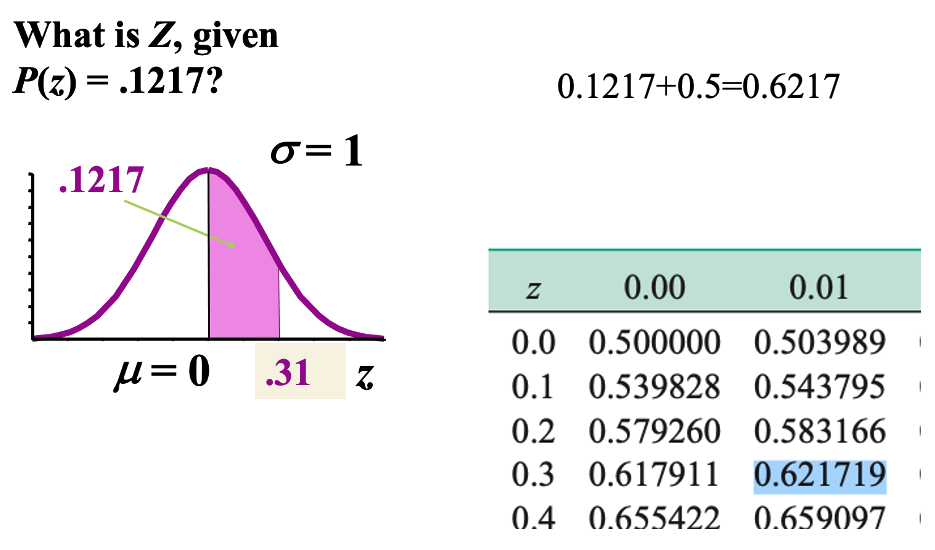
Quiz 3-4
For a particular generation of the tomato plant, the amount x of miraculin produced had a mean of 105.3 and a standard deviation of 8.0. Assume that x is normally distributed.
- Find P(100 < x < 110)
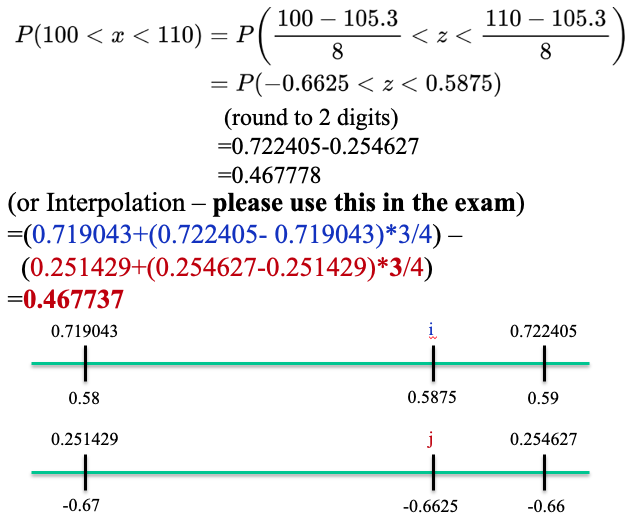
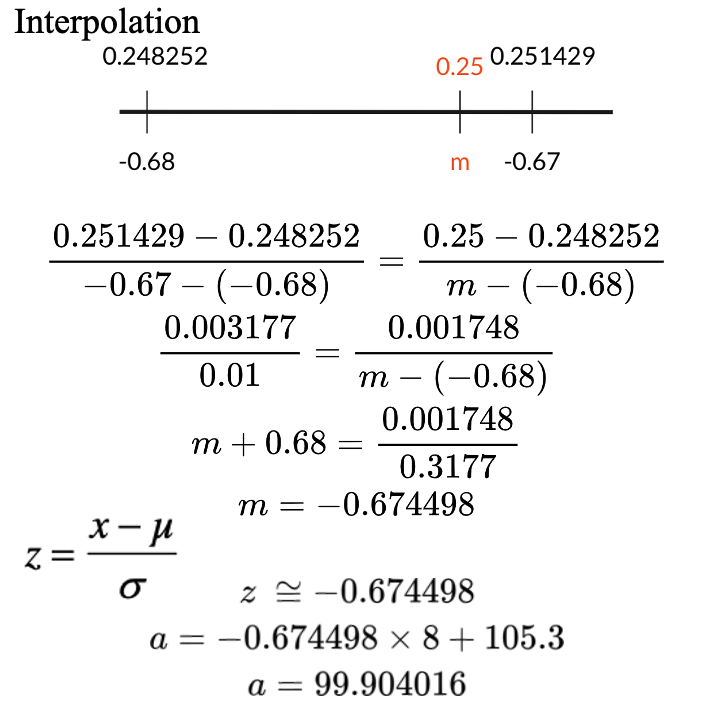
Quiz 3-4
For a particular generation of the tomato plant, the amount x of miraculin produced had a mean of 105.3 and a standard deviation of 8.0. Assume that x is normally distributed.
- Find the value a for which P(x < a) = 0.25
Is Normal Distribution a Reasonable Model?
Normal Probability Plots - load data
Import data and analyze with python using pandas. pd.read_csv("file path + name")
| name | handedness | height | weight | bavg | HR | |
|---|---|---|---|---|---|---|
| 0 | Jose Cardenal | Right | 70 | 150 | 0.275 | 138 |
| 1 | Darrell Evans | Left | 74 | 200 | 0.248 | 414 |
| 2 | Buck Martinez | Right | 70 | 190 | 0.225 | 58 |
| 3 | John Wockenfuss | Right | 72 | 190 | 0.262 | 86 |
| 4 | Tommy McCraw | Left | 72 | 183 | 0.246 | 75 |
| ... | ... | ... | ... | ... | ... | ... |
| 300 | Bob Watson | Right | 72 | 201 | 0.295 | 184 |
| 301 | Ken Harrelson | Right | 74 | 190 | 0.239 | 131 |
| 302 | Ed Charles | Right | 70 | 170 | 0.263 | 86 |
| 303 | Tony Conigliaro | Right | 75 | 185 | 0.264 | 166 |
| 304 | Phil Garner | Right | 70 | 175 | 0.260 | 109 |
305 rows × 6 columns
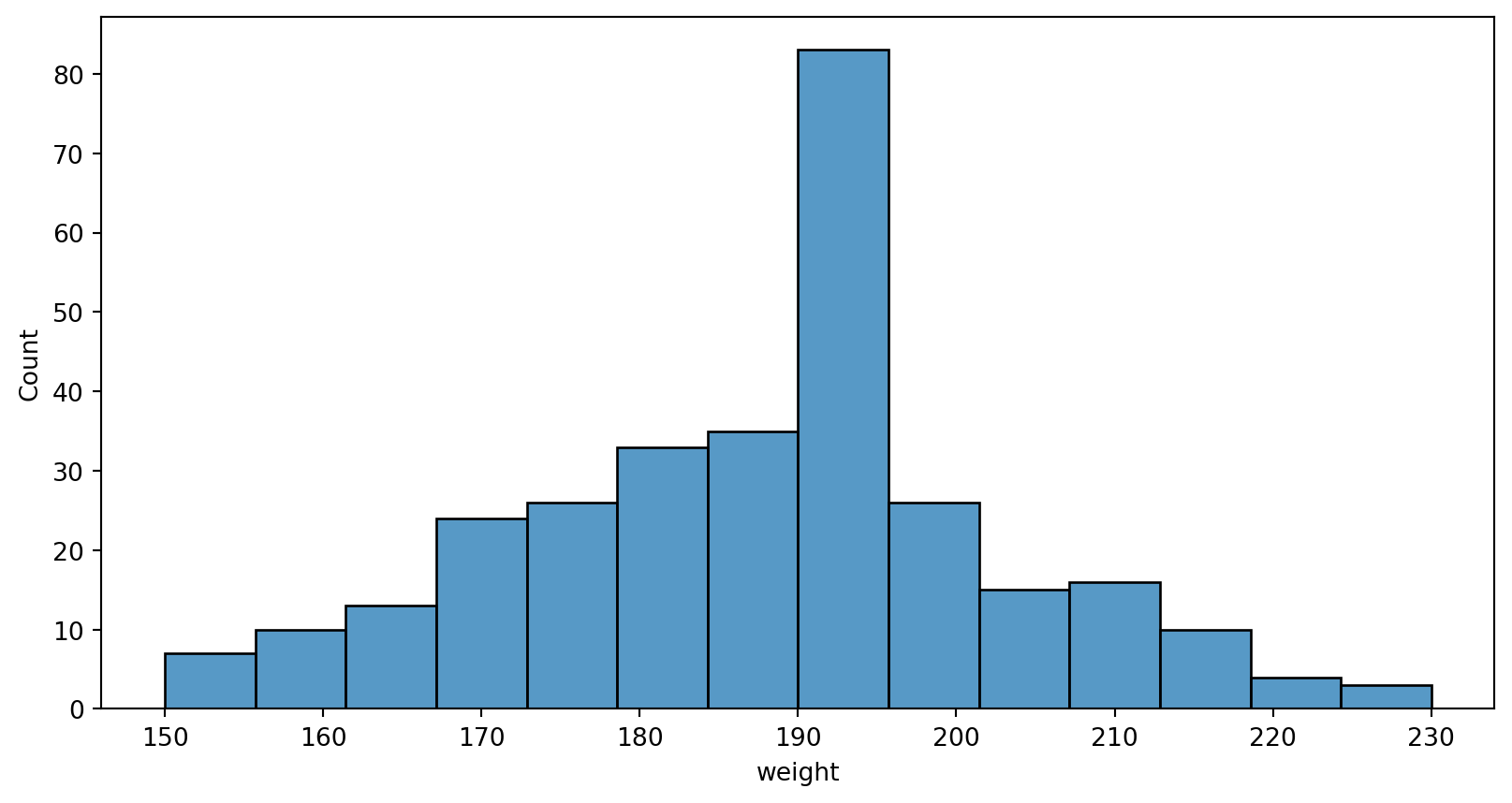
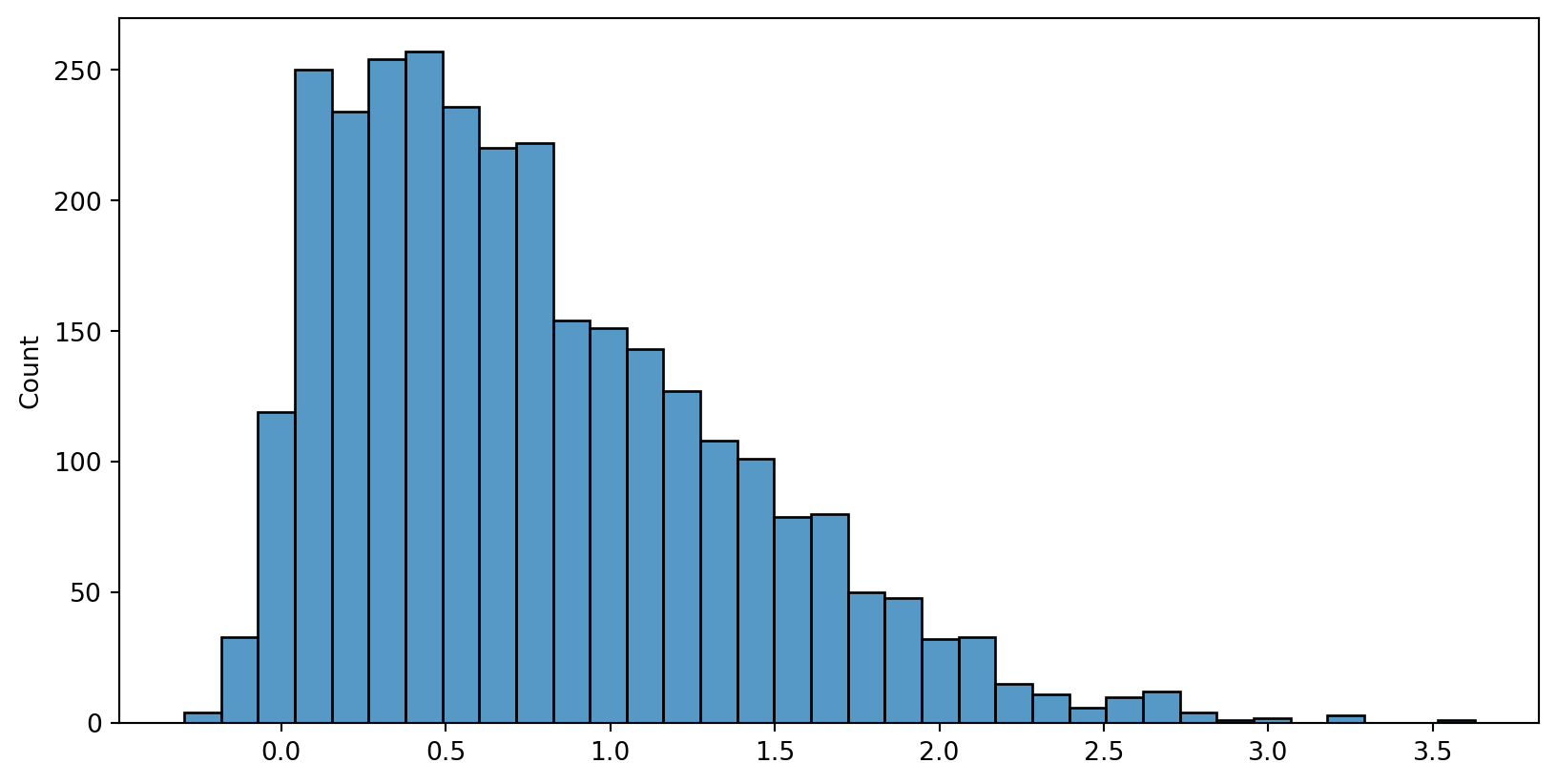
Normal Probability Plots - Histogram
seaborn package’s
histplot(data=your data frame,x=x axis)
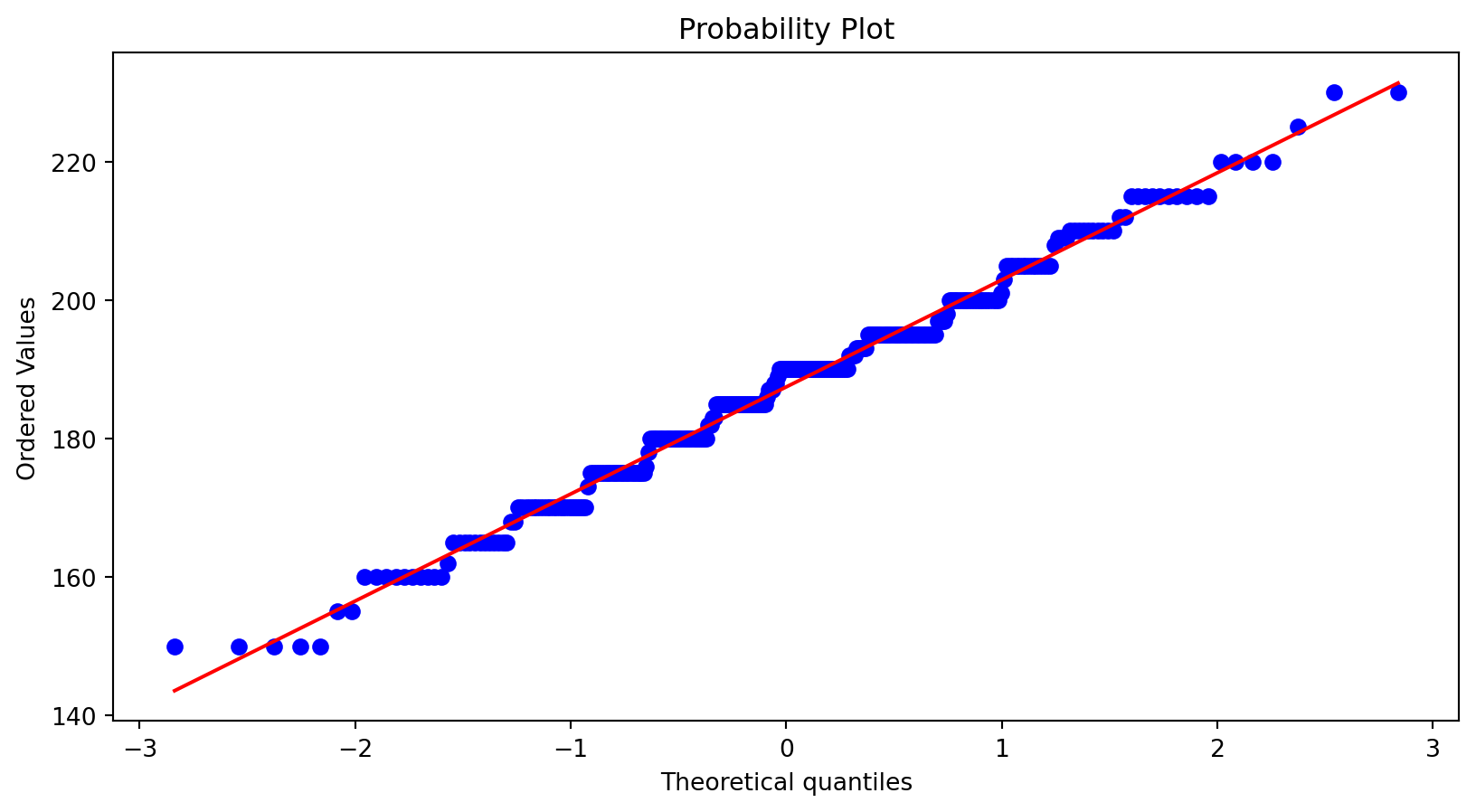
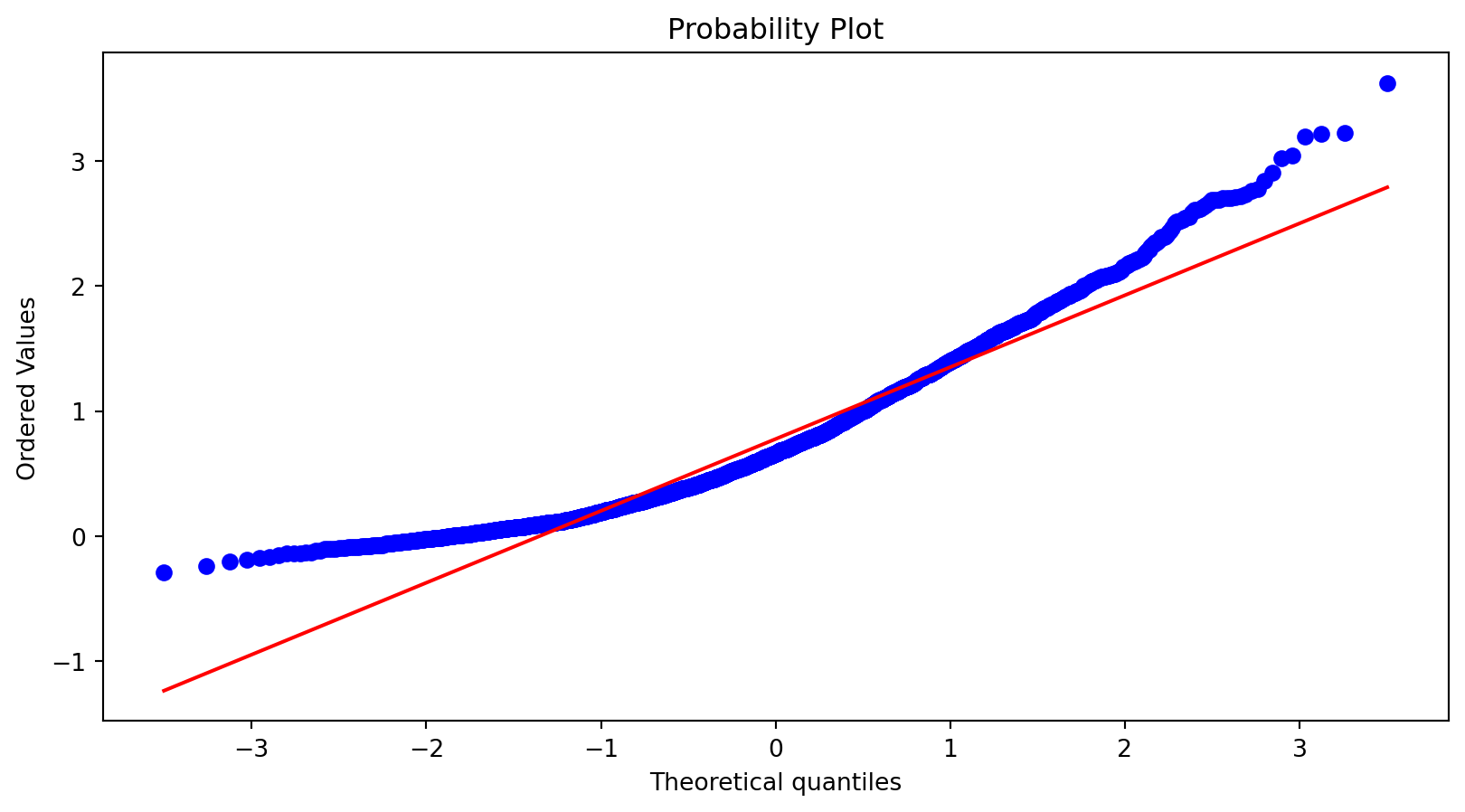
Normal Probability Plots - PP
With scipy package’s stats, we can use function probplot(data, plot=sns.mpl.pyplot) to draw Probability Plots
<Figure size 960x480 with 0 Axes>Normal Probability Plots - Histogram
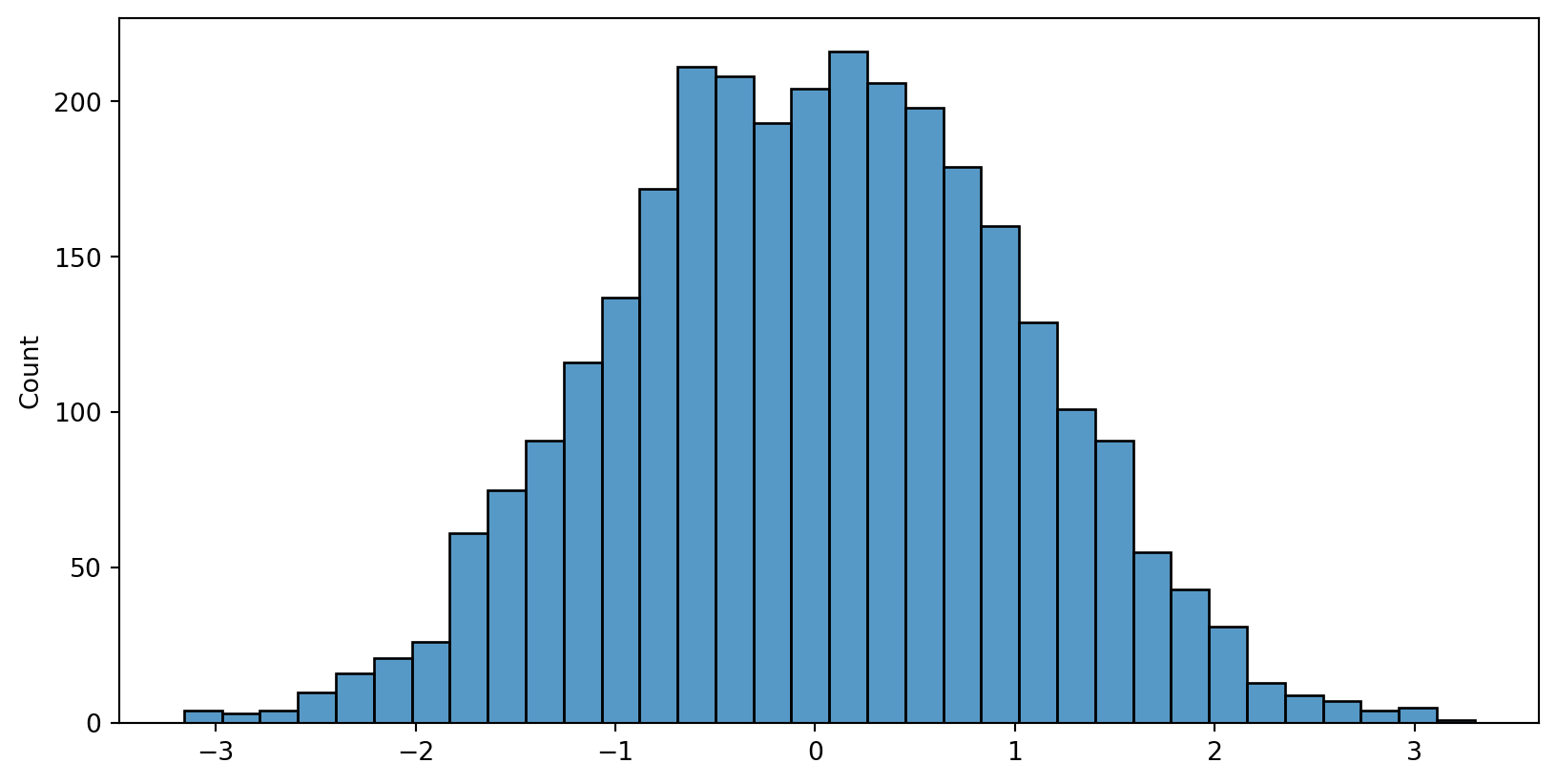
numpy’s function random.normal can be used to generate data with normal distribution
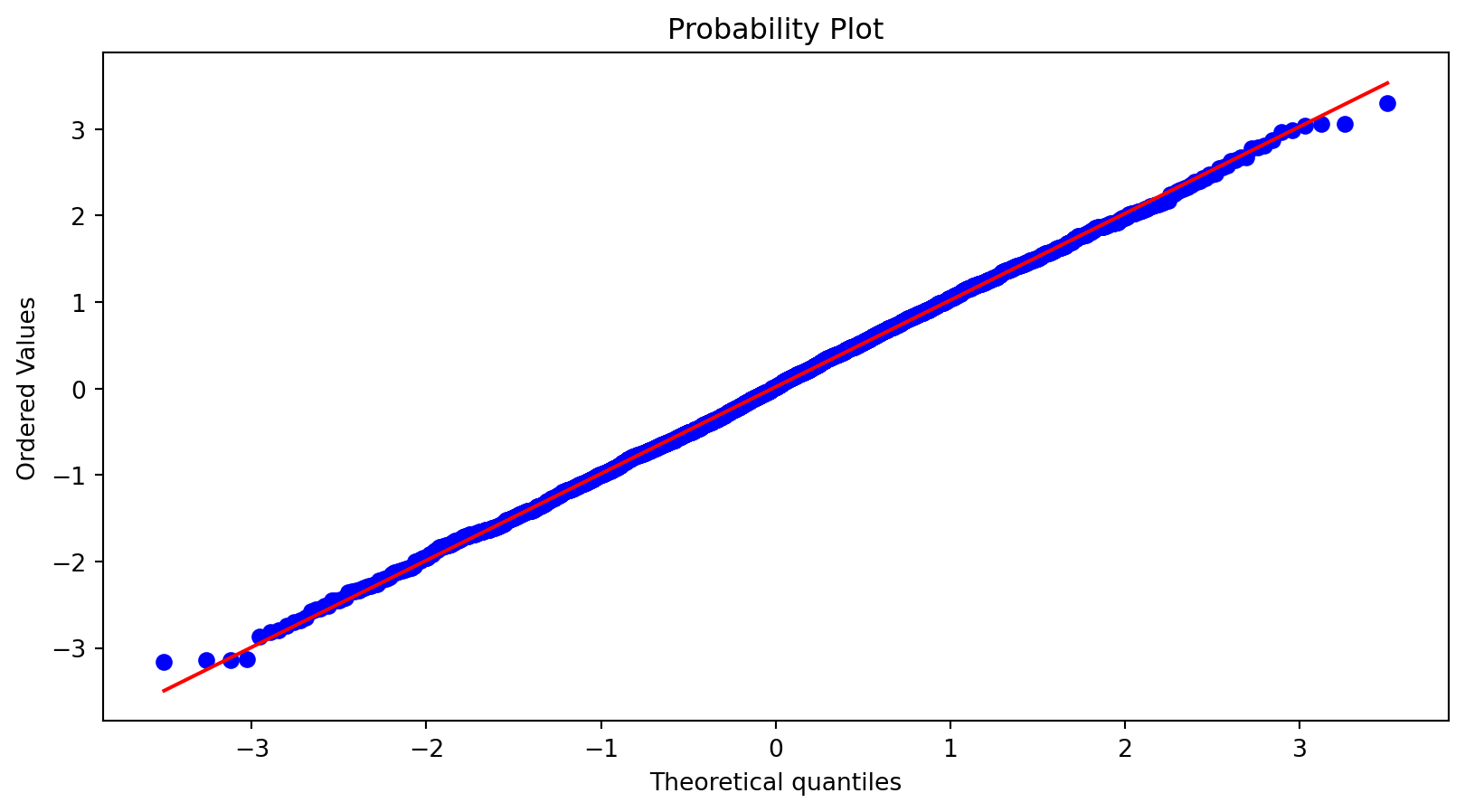
Normal Probability Plots - PP
With scipy package’s stats, we can use function probplot(data, plot=sns.mpl.pyplot) to draw Probability Plots
<Figure size 960x480 with 0 Axes>Normal Probability Plots - Histogram
With scipy package’s stats, we can use function skewnorm.rvs() to generate skewed data
Normal Probability Plots - PP
<Figure size 960x480 with 0 Axes>Statistic Test for Normal Distribution
With scipy package’s stats, the following functions can be used:
- Shapiro-Wilk Test
- May not be accurate for N > 5000
- If the p-value > .05, then the data is assumed to be normally distributed.
- Kolmogorov-Smirnov Test
- If the p-value > .05, then the data is assumed to be normally distributed.
Statistic Test for Normal Distribution
With scipy package’s stats, the following functions can be used:
- Shapiro-Wilk Test
shapiro(data) - Kolmogorov-Smirnov Test
kstest(data, distribution, args=(mean,sd))
ShapiroResult(statistic=0.9992418885231018, pvalue=0.25002941489219666)Statistic Test for Normal Distribution
With scipy package’s stats, the following functions can be used:
- Shapiro-Wilk Test
shapiro(data) - Kolmogorov-Smirnov Test
kstest(data, distribution, args=(mean,sd))
KstestResult(statistic=0.014450757533408576, pvalue=0.5530800639002007, statistic_location=-0.3566578832989416, statistic_sign=1)Binomial Distribution - Discrete Random Variables
Binomial Distribution - pmf
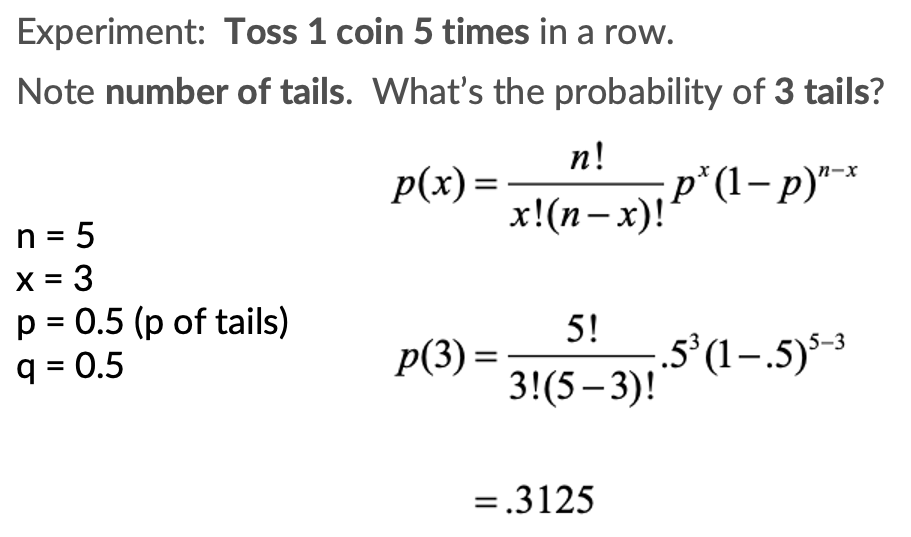
- n: number of trials
- x: number of success
- p: Probability of a ‘Success’ on a single trial
Binomial Distribution - pmf
With scipy package’s stats:
binom.pmf(x, n, p)
<Figure size 960x480 with 0 Axes>Binomial Distribution - pmf
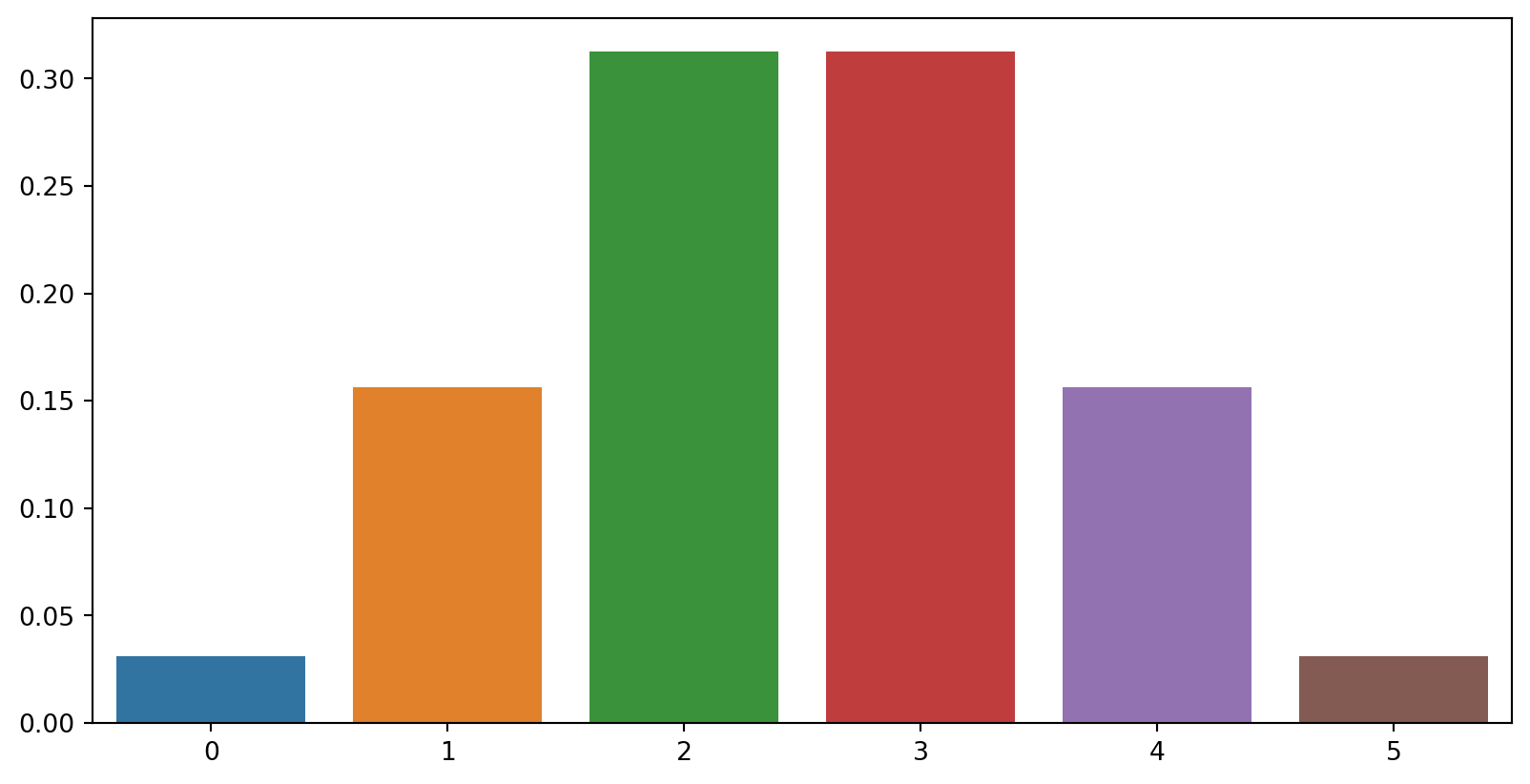
Probability (sum of the pmf)
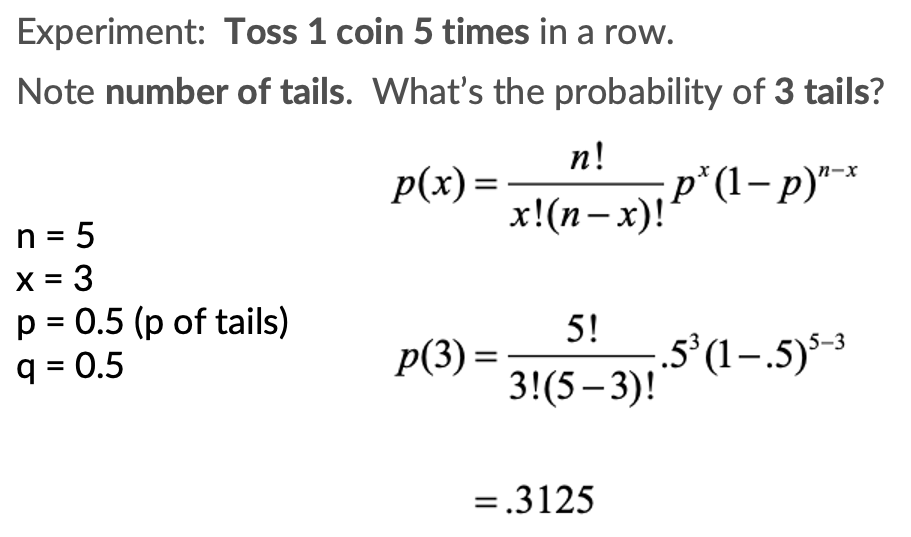
With scipy package’s stats:
binom.pmf(x, n, p)
Probability (sum of the pmf)
0.5583457484800001Quiz 3-6-a
The study found that when presented with prints from the same individual, a fingerprint expert will correctly identify the match 92% of the time.
- What is the probability that an expert will correctly identify the match in all five pairs of fingerprints?
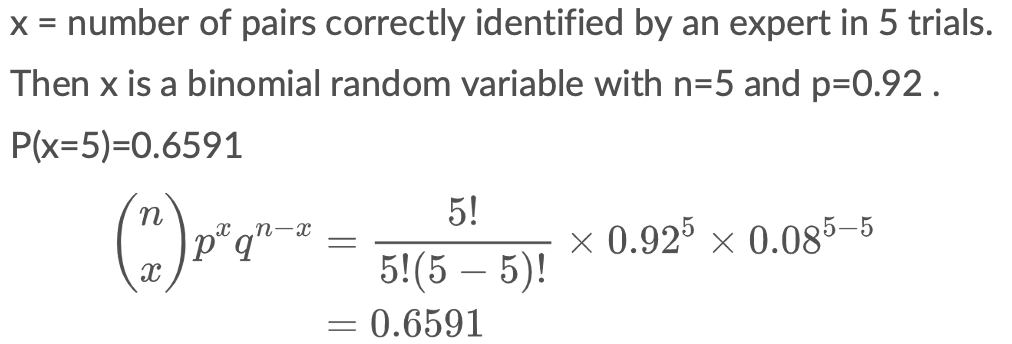
Quiz 3-6-b
In contrast, a novice will correctly identify the match 75% of the time. Consider a sample of five different pairs of fingerprints, where each pair is a match.
- What is the probability that a novice will correctly identify the match in all five pairs of fingerprints?
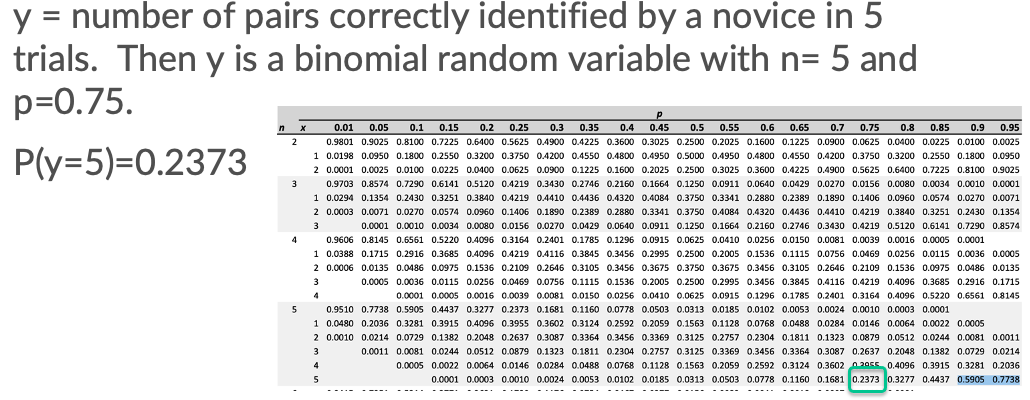
Poisson Distribution - Discrete Random Variables
Poisson Distribution - pmf

Poisson Distribution - pmf
With scipy package’s stats:
poisson.pmf(k=x, mu=λ)
<Figure size 960x480 with 0 Axes>Poisson Distribution - pmf
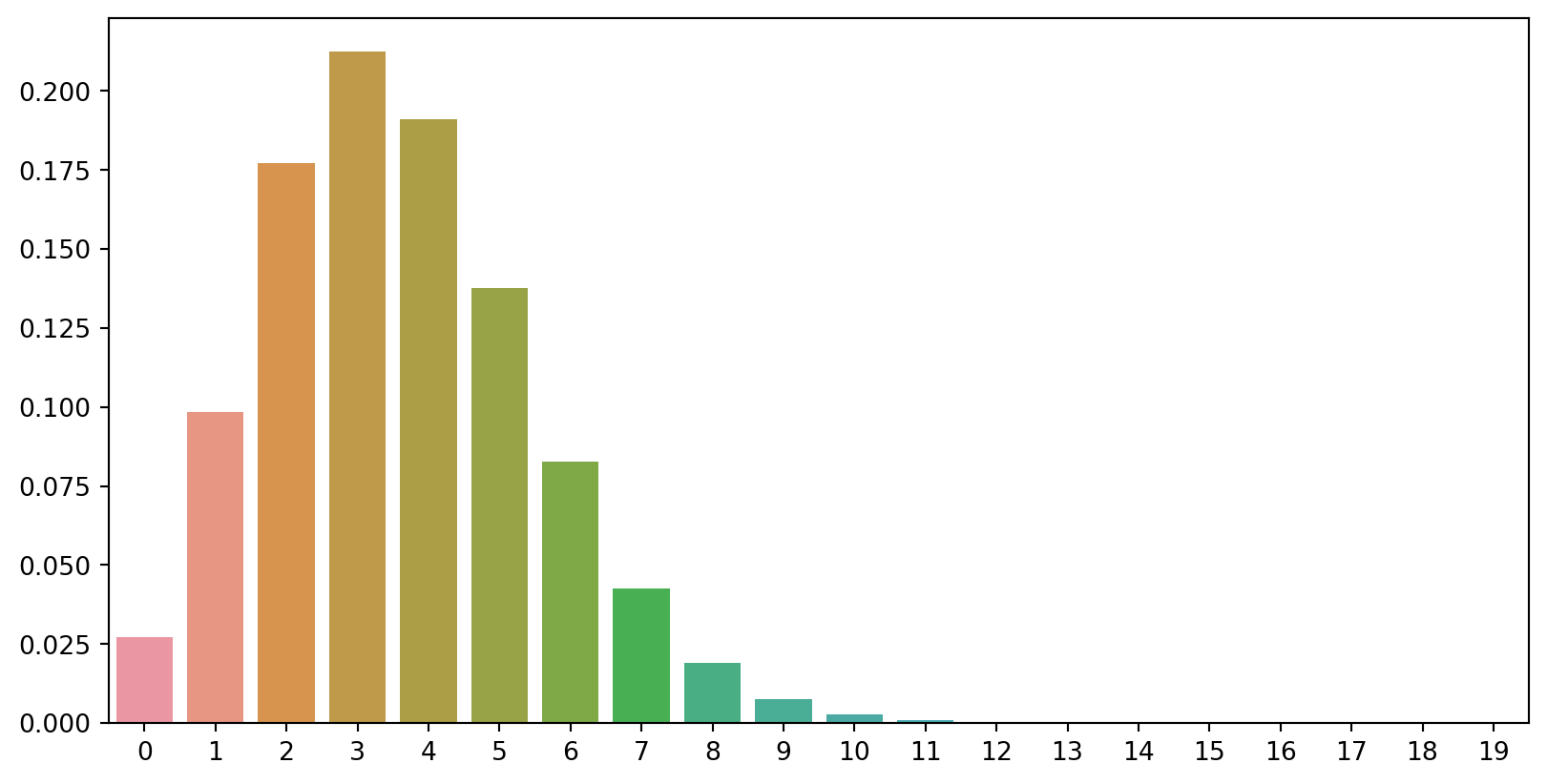
Probability (sum of the pmf)

With scipy package’s stats:
poisson.pmf(k=x, mu=λ)
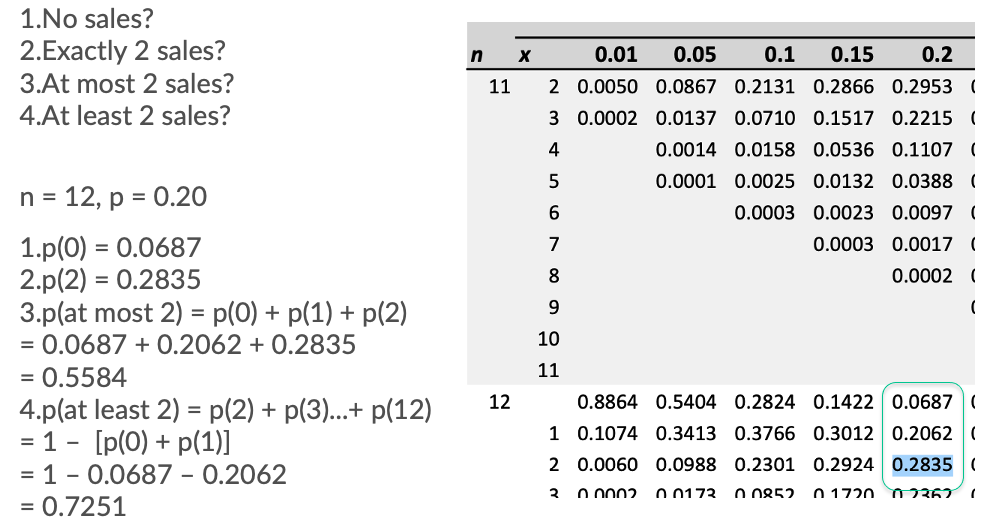
Quiz 3-8
You work in Quality Assurance for an investment firm. A clerk enters 75 words per minute with 6 errors per hour.

Exponential Distribution - Continuous Random Variables
Probability (area under the pdf)

With scipy package’s stats:
expon.cdf(x, scale=θ)
Quiz 3-9
the length of life of a magnetron tube has an exponential probability distribution with θ = 6.25.
Suppose a warranty period of 5 years is attached to the magnetron tube. What fraction of tubes must the manufacturer plan to replace?
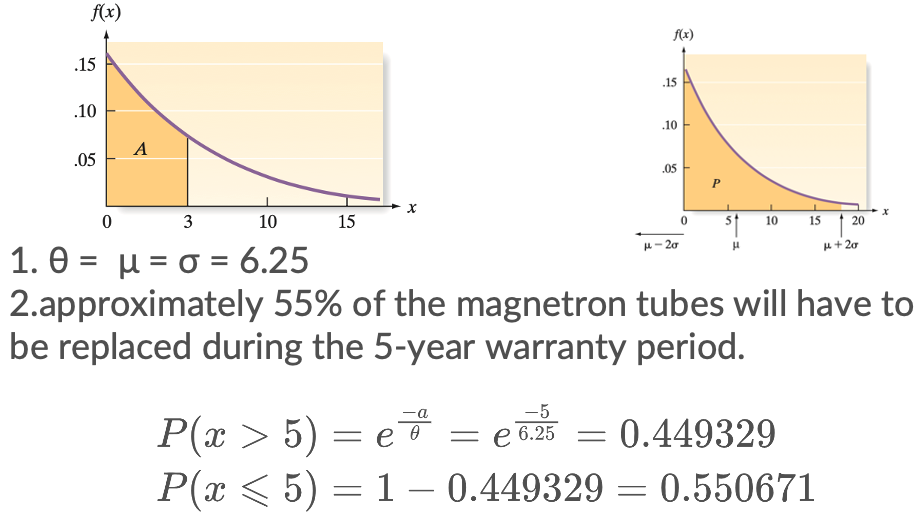
Summary
- Normal Distribution
NormalDist(mu=μ, sigma=σ).cdf(x)- Probability Plot
- Statistic Test
- Binomial Distribution
binom.pmf(x, n, p) - Poisson Distribution
poisson.pmf(k=x, mu=λ) - Exponential Distribution
expon.cdf(x, scale=θ)